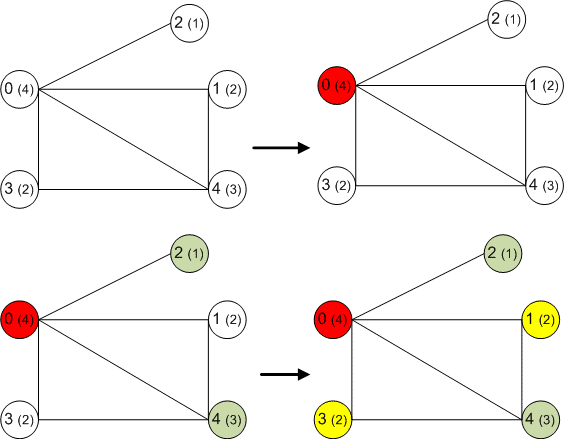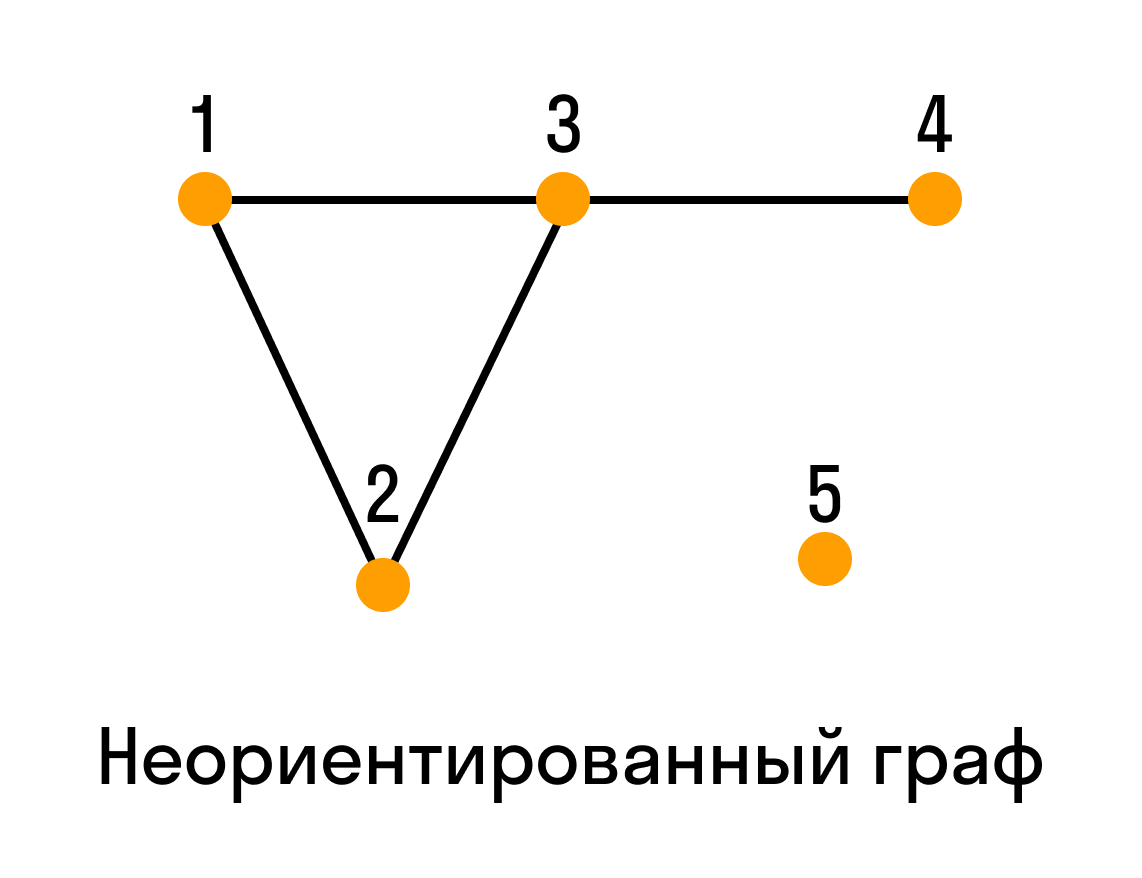
Занятие «Раскраски графов» факультативного курса «Элементы теории графов и ее приложения»
Теорема о четырех цветах — это математический вопрос, который возник еще в 19 веке. Он заключается в том, можно ли раскрасить любую карту, используя только четыре цвета, таким образом, чтобы ни одна из двух соседних областей не имела одинакового цвета. В этом материале мы расскажем, у кого впервые возник этот вопрос, причем тут теория графов, кто и как пытался доказать эту теорему и что из этого вышло.
![Похожие статьи [В работе] Конспект лекции по раскраскам](https://image.slidesharecdn.com/random-131116113252-phpapp02/85/-12-320.jpg)




Сайт заблокирован хостинг-провайдером. Вы владелец сайта? Информация о причинах блокировки была выслана на Ваш контактный E-mail. Также Вы можете связаться с нашей службой технической поддержки с помощью раздела "Помощь и поддержка" в панели управления хостингом или любым удобным для Вас способом. This page is blocked by service provider.
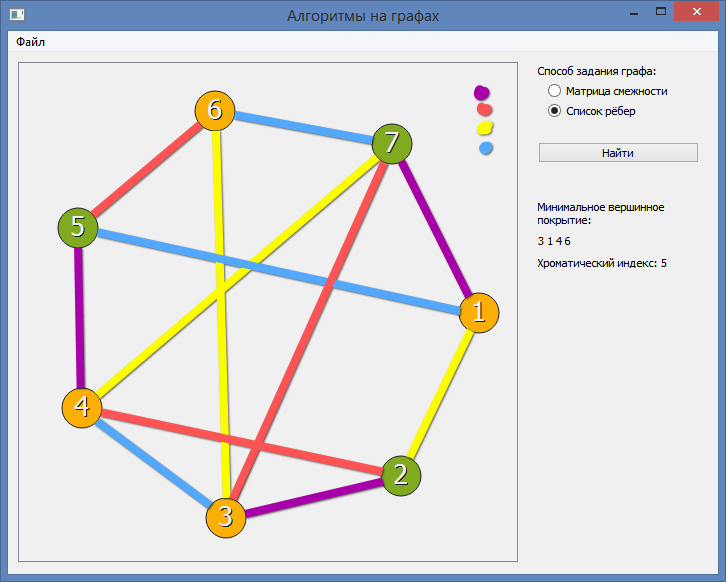
- Алгоритм последовательной раскраски
- Работа выполнена в Учреждении Российской академии наук Институте математики им. Соболева Сибирского отделения РАН.
- Попробуйте повторить позже.
- В этом уроке мы разберем, что такое раскраска графов и как это относится к цифрам на вершинах.


![Публикации [В работе] Конспект лекции по раскраскам [МОЭВМ Вики [allegrosad.ru]]](https://habrastorage.org/getpro/habr/upload_files/d86/1a5/6f3/d861a56f3a53e3acef2083daf91c1a0f.png)
| 437 | Регистрация Выслать повторно письмо для активации Что даёт регистрация на форуме? Форум на Исходниках. | |
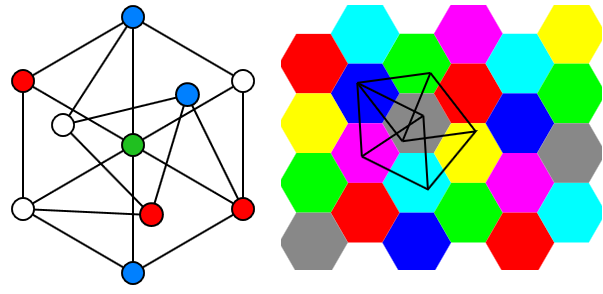
| 298 | Первоначально раскраски графов были нужны для составления географических карт [1]. Сегодня же они в частности раскраска с использованием минимального количества цветов используются, например, для составления расписаний, распределения регистров в микропроцессорах, распараллеливания численных методов. | |
| 326 | Ваши алгоритмы не работают на графах с одинаковыми степенями вершин. Собственно успешность алгоритма зависит от того с какой вершины начать. | |
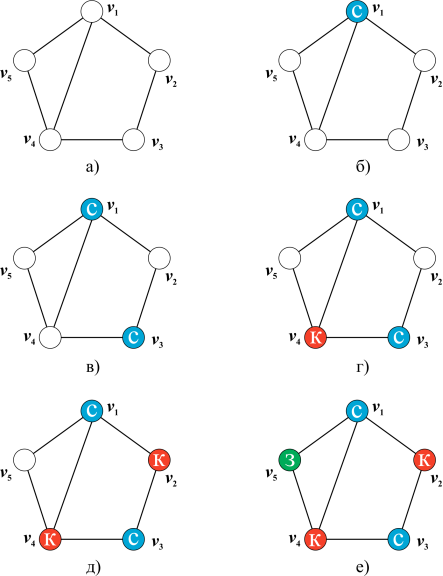
| 295 | Когда говорят о раскраске графов, почти всегда подразумевают под этим раскраску их вершин, то есть присвоение цветовых меток вершинам графа так, чтобы любые две вершины, имеющие общее ребро, имели разные цвета. Так как графы, в которых есть петли, не могут быть раскрашены таким образом, они не являются предметом обсуждения. | |
| 402 | В этой небольшой заметке я хочу показать, как с помощью алгебры можно решать классическую задачу о раскраске вершин графа. |
На этом шаге мы рассмотрим алгоритмы закраски графа. Задачи определения хроматического числа и построения минимальной раскраски произвольного графа являются очень сложными. С одной стороны, не известны алгоритмы их решения, сложность которых есть некоторая фиксированная степень от длины записи условий задачи так называемые полиномиальные алгоритмы. С другой стороны, нигде явно не выражены те потери, которые мы несем от отсутствия таких алгоритмов [1, с. Разумеется, есть лишь конечное число ситуаций, которые надо рассмотреть, чтобы найти хроматическое число n -вершинного графа.